Grassmann algebra is an algebra for Geometry
The simple algebraic entities of Grassmann algebra may be
interpreted as points, lines, planes, vectors, bivectors and
trivectors, and their multidimensional variants. This
interpretation imbues the product operations of the algebra
with a concomitant geometric significance.
On this page we display a series of graphics from Volume 1 using the
entities and operations of the algebra as direct inputs to the drawing
routines. Operations include the exterior product for combining
entities, and the regressive product for finding their common
components. The entities of the algebra can represent vectors,
bivectors and multivectors, points, lines, planes, and multiplanes.
Projective geometry of n-space is subsumed by the algebra, and many
of its theorems reduced to the vanishing of products of the entities.
From these entities, higher order objects can be defined: for example
curves, surfaces, simplexes or regions of space. Expressions involving
these may often be considered as a prescription to construct them.
Grassmann algebra is an algebra par excellence for geometry.
Animated with systems like Mathematica it also has the potential to
become an algebra for dynamic simulations in fields such as physics,
engineering and game development.
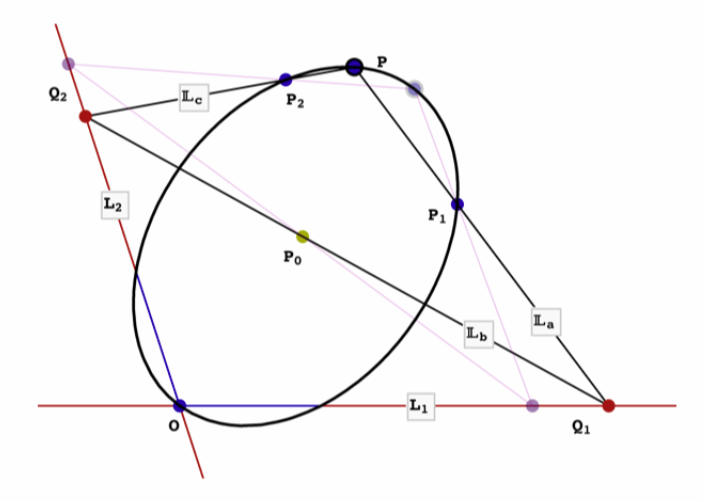
Constructing conics in space
This graphic shows the conic formed from two points, a line, and two planes according to an equation in which P is the variable point describing the conic. Note that since a conic is of second degree, the variable point P occurs twice in the product. The product itself involves both the exterior product operation for building entities, and the regressive product operation for intersecting them.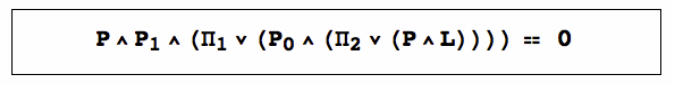


© John Browne 2018.
[ Home ] [ Biography ] [ Bibliography ] [ Book Contents ] [ Chapter 1 PDF ] [ Geometry ] [ Book ] [ Contact ]

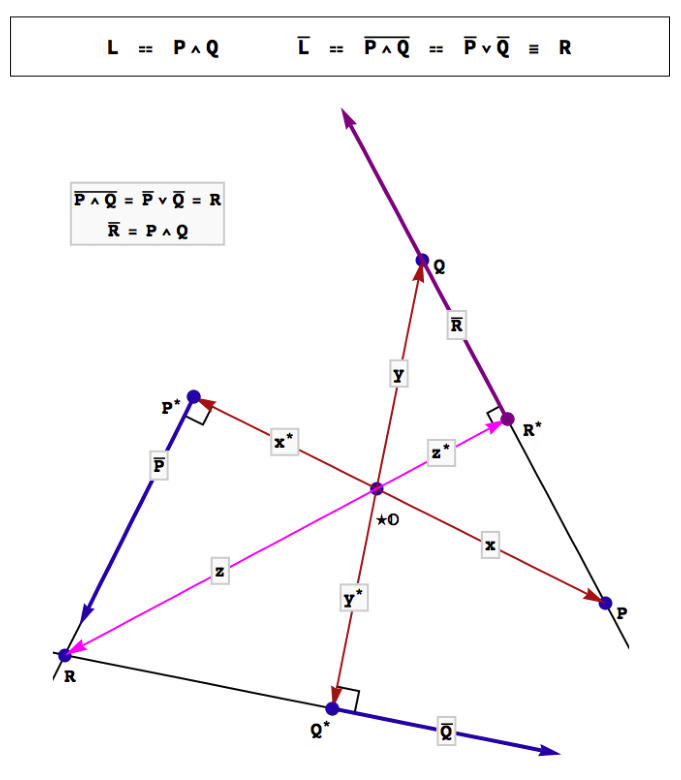
Complements of points and lines in the plane
In the plane, the complement of a point is a line, and the complement of a line is a point. If a line is defined by two points, then its complement is the intersection of the complements of the points. The graphic below shows these relationships, with x, y and z the position vectors of three points. Inverses of points and vectors are indicated with *-superscripts. In higher dimensional spaces, the same relationships hold but their interpretations are different. For example in a bound 3-space the complement of a point is a plane and the complement of a plane is a point. The complements of two points P and Q yield two planes which intersect in a line R whose complement passes through the points P and Q.
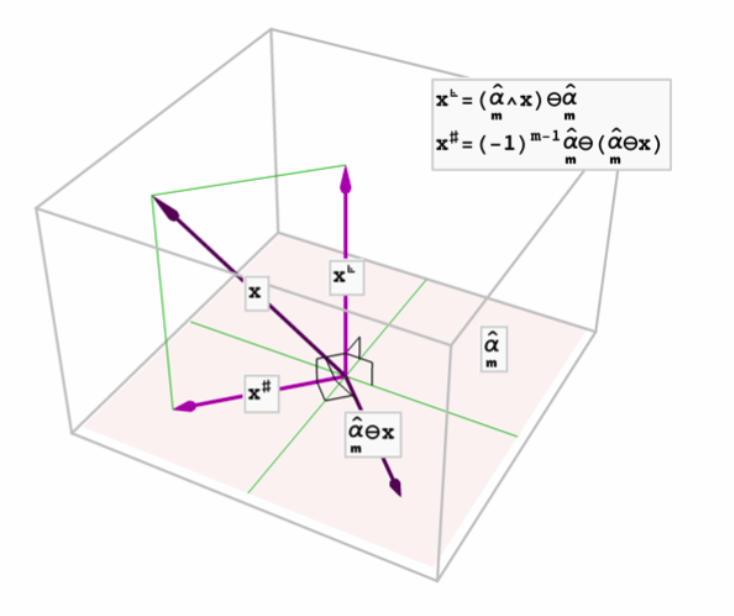
The triangle components
Given a simple unit multivector, any vector x may always be decomposed into the sum of two components: one orthogonal to the multivector, and one parallel to it.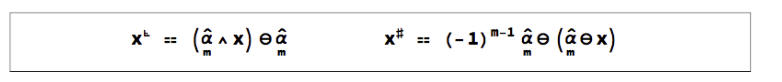

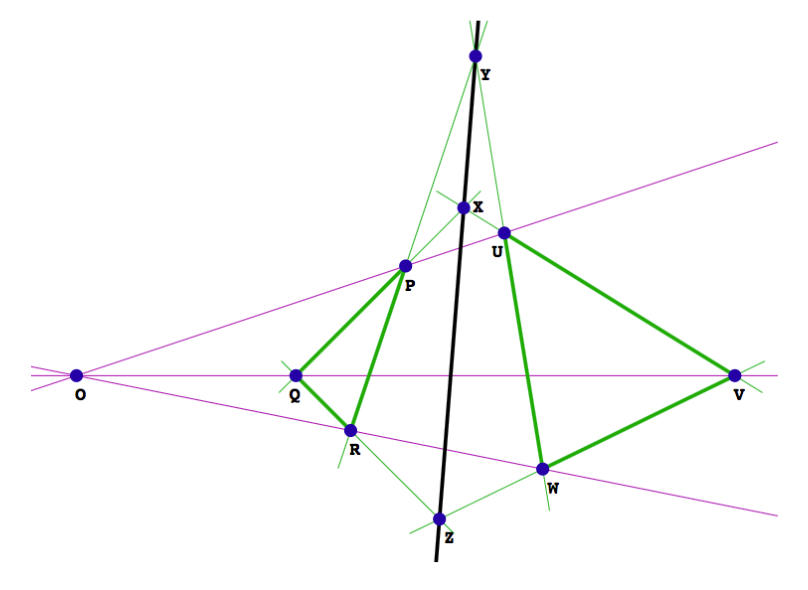
Desargues’ Theorem
Desargues' Theorem states that If two triangles have corresponding vertices joined by concurrent lines, then the intersections of corresponding sides are collinear. That is, if PU, QV and RW all pass through one point O, then the intersections X = PQ.UV, Y = PR.UW and Z = QR.VW al lie on one line. As Grassmannian equations, these conditions translate to

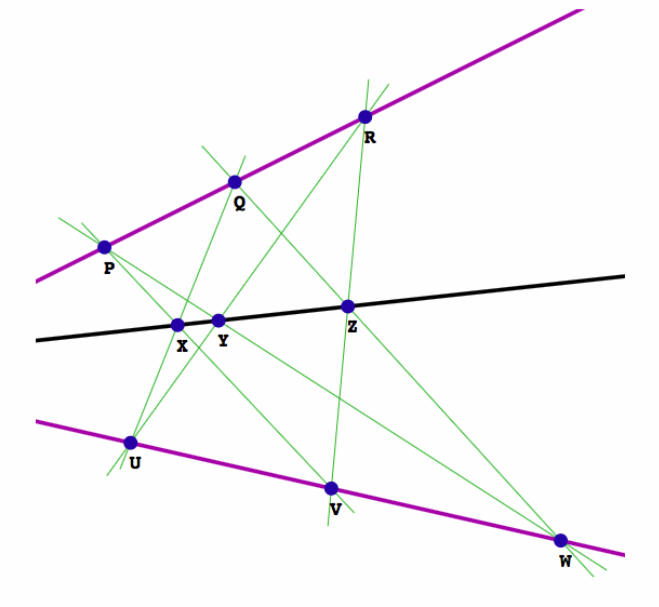
Pappus’ Theorem
Pappus' Theorem states that Given two sets of collinear points P, Q, R and U, V, W, then the intersection points X, Y, Z of the lines PV and QU, PW and RU, QW and RV, are collinear. As Grassmannian equations, these conditions translate to





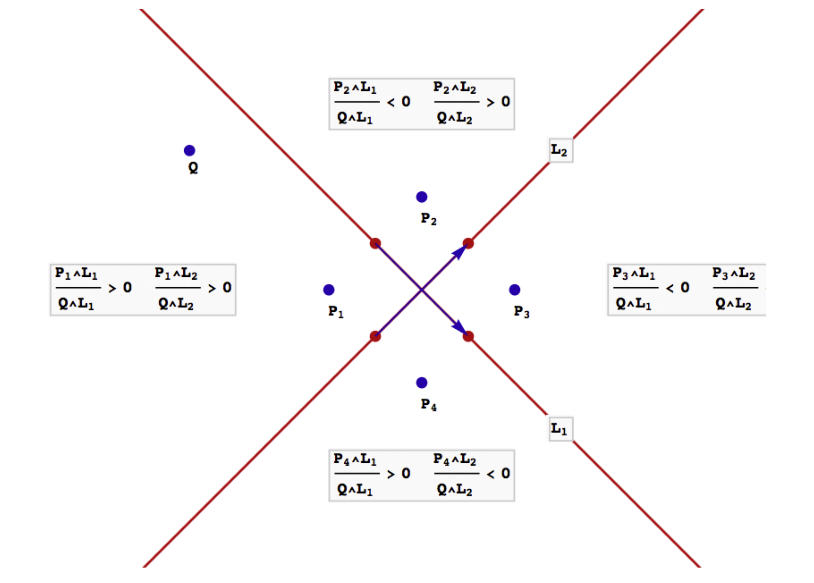
Regions defined by two lines in the plane
To define the four regions of a plane defined by two non-parallel lines we only need to know the location of one point, Q say. All products of a point and a line in the plane are congruent, so quotients of them can be defined as the quotients of their scalar multiples. These quotients may be positive or negative. The four regions of the plane correspond to the four combinations of the signs + and - with the region containing Q corresponding to (+, +). To see if a point P lies in the same quadrant as a point Q evaluate the conjunction of their inequalities.


Creating a 5-star pyramid
We are not constricted to the plane when it comes to defining regions. In an n-space, a hyperplane divides its space into two regions. If two points lie on the same side of a hyperplane H, then the ratio R of the exterior products of the two points with H is positive. If the points lie on opposite sides of H then R is negative. If the point in the numerator lies on the hyperplane then R is zero. Regions of space may be defined by logical functions of the predicates R > 0, R < 0, R = 0, R >= 0, and R <= 0. The graphic below shows a pyramid with a 5-star base defined by 5 points, and 5 hyperplanes (in this case planes) through two points and the vertex.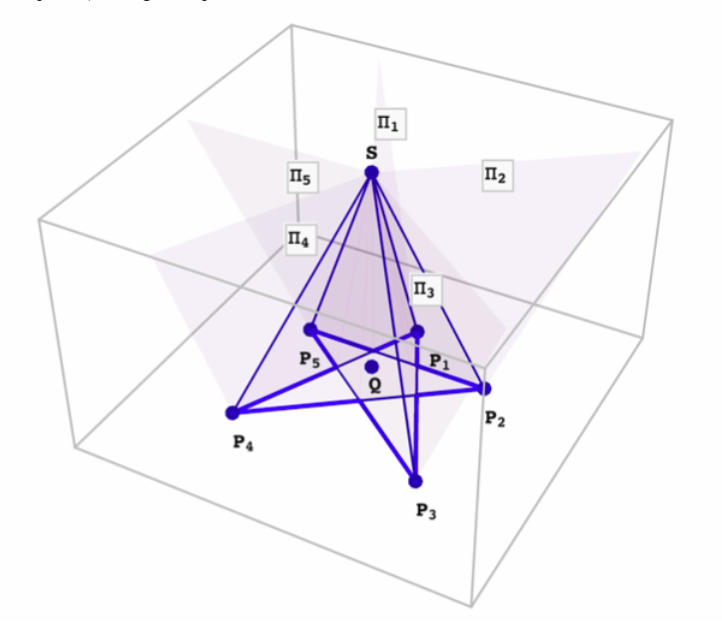

The geometric equation as a prescription to construct
A geometric equation, either as a series of steps, or in its final form can be used as a prescription to construct a curve or surface. In the case below, the equation can be viewed as a prescription to construct a conic section in the plane. An exterior product of points means "draw a line through the points". A regressive product of lines means "find their point of intersection". Construct an ellipse from the equation below by working from left to right.