This site introduces the first of two printed volumes on the work of Hermann

Grassmann as it re-emerges from one and a half centuries of isolation.

The books have grown out of an interest in Grassmann's work over the past four decades. There is something fascinating about the beauty with which the mathematical structures Grassmann discovered (invented, if you will) describe the physical world, and something also fascinating about how these beautiful structures have been largely lost to the mainstreams of mathematics and science. Volume 1: Foundations - develops the algebraic foundations of the structures. Volume 2: Extensions - will explore some of their extensions to other systems.

The genesis of Grassmann algebra

Hermann Günther Grassmann was born in 1809 in Stettin, near the border of Germany and Poland. He was only 23 when he discovered the method of adding and multiplying points and vectors which was to become the foundation of his Ausdehnungslehre. In 1839 he composed a work on the study of tides entitled Theorie der Ebbe und Flut, which was the first work ever to use vectorial methods. In 1844 Grassmann published his first Ausdehnungslehre (Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik) and in the same year won a prize for an essay which expounded a system satisfying an earlier search by Leibniz for an 'algebra of geometry'. Despite these achievements, Grassmann received virtually no recognition. In 1862 Grassmann re-expounded his ideas from a different viewpoint in a second Ausdehnungslehre (Die Ausdehnungslehre. Vollständig und in strenger Form). Again the work was met with resounding silence from the mathematical community, and it was not until the latter part of his life that he received any significant recognition from his contemporaries. Of these, most significant were J. Willard Gibbs who discovered his works in 1877 (the year of Grassmann's death), and William Kingdon Clifford who discovered them in depth about the same time. Both became quite enthusiastic about this new mathematics. More details on the biography of Grassmann may be found on the Biography page of this site, but for the most comprehensive biography see Petsche [2009] on the same page.

The power of Grassmann algebra

The intrinsic power of Grassmann algebra arises from its fundamental product operation, the exterior product. The exterior product codifies the property of linear dependence, so essential for modern applied mathematics, directly into the algebra. Simple non-zero elements of the algebra may be viewed as representing constructs of linearly independent elements. For example, a simple bivector is the exterior product of two vectors; a line is represented by the exterior product of two points; a plane is represented by the exterior product of three points.

The focus of the Grassmann algebra books

The focus of these two volumes is to provide a readable account in modern notation of Grassmann's major algebraic contributions to mathematics and science in a form accessible to scientists and engineers, students and professionals alike. Consequently mathematical terminology which does not make an essential contribution to understanding the basic concepts has been avoided. The only assumption made as to the reader's background is that they have some familiarity with basic linear algebra. The focus is also to provide an environment for exploring applications of Grassmann algebra. For general applications in higher dimensional spaces, computations by hand in any algebra become tedious, indeed limiting, thus restricting the hypotheses that can be explored. For this reason the volumes are integrated with a Mathematica package called GrassmannAlgebra. You can read the book without using the package, or you can use the package to extend the examples in the text, experiment with hypotheses, or explore your own interests. To get a copy of the GrassmannAlgebra package, see the Contact page.

Volume 1: Foundations

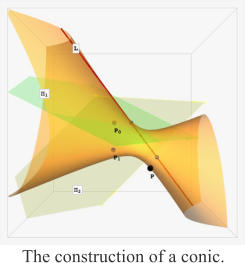
Volume 1: Foundations comprises six chapters. Chapter 1 provides a brief preparatory overview, introducing the seminal concepts of each chapter, and solidifying them with simple examples. This chapter (which can be downloaded from this site) is designed to give you a global appreciation with which better to understand the detail of the chapters which follow. However, it is independent of those chapters, and may be read as far as your interest takes you. Chapter 2 discusses the exterior product - the fundamental product operation of the algebra - and shows how it creates the suite of linear spaces which form the algebra. Chapter 3 discovers that the symmetry in this suite leads to another product, the regressive product, elegantly 'dual' to the exterior product. Equipped with these dual products, Chapter 4 shows how the algebra can be interpreted geometrically to easily recreate projective geometry. The construction of the conic shown is an example. Chapter 5 lays the foundation for introducing a metric by defining for each element, a partner - its complement. Then Chapter 6 shows how to combine all of these to define the interior product, a much more general product than the scalar product. These chapters form the essential core for a working knowledge of Grassmann algebra and its extensions in the second volume. They are most profitably read (or at least scanned) sequentially. The rest is exploration!

Volume 2: Extensions

Volume 2: Extensions is currently a work in progress. When it is published you will find explorations using the fundamental theory developed in this volume extended to other topics, for example the generalized product, and to other branches of mathematics, for example the hypercomplex and Clifford algebras.

Acknowledgements

Writing these sorts of books also involves a lot of Mathematica coding. In this I would like to especially acknowledge my great appreciation of David Park's interest in Grassmann algebra and Grassmann calculus and the thought-provoking conversations which have ensued. Particularly, I would like to acknowledge his many contributions to the GrassmannAlgebra and GrassmannCalculus software packages. To get a copy of these packages, see the Contact page. Above all however, I must acknowledge Hermann Grassmann. His contributions to mathematics and science put him among the great thinkers of the nineteenth century. I hope you enjoy exploring this beautiful mathematical system. John Browne October, 2012

More than 150 years ago - Hermann Grassmann made a prophecy

“For I have every confidence that the effort I have applied to the science reported upon here, which has occupied a considerable span of my lifetime and demanded the most intense exertions of my powers, is not to be lost. … a time will come when it will be drawn forth from the dust of oblivion and the ideas laid down here will bear fruit. … some day these ideas, even if in an altered form, will reappear and with the passage of time will participate in a lively intellectual exchange. For truth is eternal, it is divine; and no phase in the development of truth, however small the domain it embraces, can pass away without a trace. It remains even if the garments in which feeble men clothe it fall into dust.” Hermann Grassmann - in the foreword to the Ausdehnungslehre of 1862, translated by Lloyd Kannenberg.